Κλασική Θεωρία Ελέγχου

Στόχος της ενότητας αυτής είναι να εισαγάγει τον φοιτητή στην έννοια του σήματος και του συστήματος μέσα από πολλά παραδείγματα ιστορικά αλλά και της καθημερινότητας. Γίνεται ο διαχωρισμός των δύο κατηγοριών συστημάτων : συστήματα ανοικτού βρόγχου και συστήματα κλειστού βρόγχου. Παρουσιάζονται πλεονεκτήματα και μειονεκτήματα της κάθε κατηγορίας συστημάτων. Στο τέλος τίθενται οι στόχοι της Θεωρίας Ελέγχου.

Στην ενότητα αυτή παρουσιάζονται τα σήματα συνεχούς χρόνου που θα χρησιμοποιηθούν κυρίως στις επόμενες ενότητες καθώς και η έννοια της χρονικής μετάθεσης σήματος. Παρουσιάζεται επίσης η έννοια της γενικευμένης παραγώγου.

Στην τρίτη ενότητα παρουσιάζεται η γενική περιγραφή ενός συστήματος στον χώρο των καταστάσεων και η ειδική της μορφή στην περίπτωση των γραμμικών συστημάτων. Δίνονται αρκετά παραδείγματα από ηλεκτρικά και μηχανικά συστήματα. Τέλος δίνεται ο τρόπος αναπαράστασης των εξισώσεων που περιγράφουν ένα σύστημα στην γενική μορφή που αναπτύχθηκε προηγουμένως. Γίνεται επίσης μια σύντομη περιγραφή της γραμμικοποίησης ενός μη γραμμικού συστήματος.

Στην τέταρτη ενότητα παρουσιάζονται βασικές ιδιότητες συστημάτων π.χ. αιτιότητα, γραμμικότητα κ.λ.π.

Βασικό εργαλείο για την επίλυση συστημάτων διαφορικών εξισώσεων αλλά και την περιγραφή συστημάτων αποτελεί ο μετασχηματισμός Laplace συναρτήσεων. Στην πέμπτη ενότητα δίνεται ο ορισμός του μονόπλευρου μετασχηματισμού Laplace και με την βοήθεια αυτού υπολογίζουμε τον μετασχηματισμό Laplace γνωστών συναρτήσεων. Στη συνέχεια μελετούμε ιδιότητες του μετασχηματισμού Laplace.

Οι μετασχηματισμοί Laplace ανάγουν τα προβλήματα επίλυσης συστημάτων διαφορικών εξισώσεων σε αλγεβρικά συστήματα των οποίων οι λύσεις συνήθως είναι ρητές συναρτήσεις. Το τελικό αποτέλεσμα που ψάχνουμε είναι ο αντίστροφος μετασχηματισμός Laplace των ρητών αυτών συναρτήσεων. Στην έκτη ενότητα εισάγουμε τεχνικές υπολογισμού του αντίστροφου μετασχηματισμού Laplace συναρτήσεων.

Στην ενότητα αυτή μελετούμε διάφορα είδη αποκρίσεων ενός συστήματος όπως : α) κρουστική απόκριση, β) βηματική απόκριση και γ) αρμονική απόκριση.

Στην ενότητα αυτή μελετούμε δύο κατηγορίες συστημάτων : α) συστήματα πρώτης τάξης και β) συστήματα δεύτερης τάξης.

Στην ένατη ενότητα δίνεται η περιγραφή ενός συστήματος στο πεδίο της συχνότητας δηλ. μέσω της συνάρτησης μεταφοράς του.

Στην ενότητα αυτή παρουσιάζονται αλγεβρικά κριτήρια ευστάθειας (Routh-Hurwitz, Lienard-Chipart). Τα κριτήρια αυτά προσδιορίζουν χωρίς να υπολογίζουν τα μηδενικά ενός πολυωνύμου αν αυτά βρίσκονται στο αριστερό μιγαδικό επίπεδο. Τα κριτήρια αυτά γενικεύονται στην περίπτωση που έχουμε διαστηματικά πολυώνυμα από το θεώρημα Kharitonov.

Σε αυτή την ενότητα προτείνουμε μια μεθοδολογία για την σχεδίαση του γεωμετρικού τόπου των ριζών ενός πολυωνύμου της μορφής d(s)+k*h(s) για όλες τις τιμές του πραγματικού αριθμού k (d(s), h(s) γνωστά πολυώνυμα). Ο γεωμετρικός τόπος των ριζών είναι ένα βασικό εργαλείο που ανακαλύφθηκε από τον Walter Richard Evans το 1948 και έχει ως στόχο την μελέτη της ευστάθειας συστημάτων.

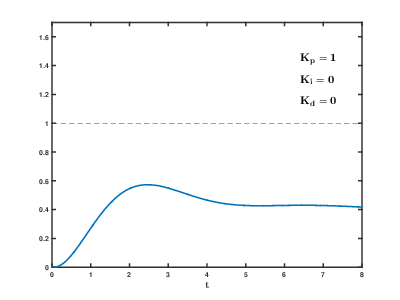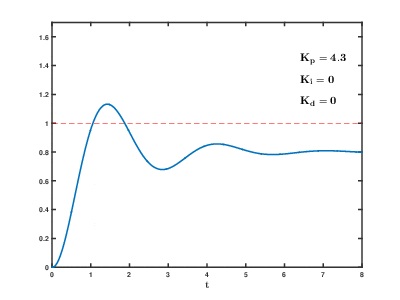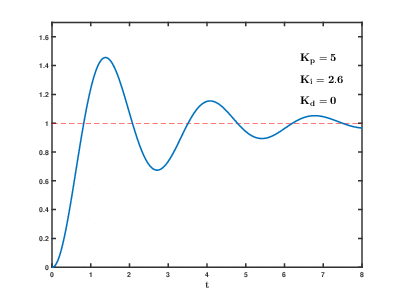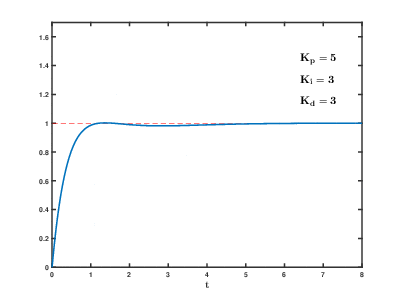
• Ποσοστό Υπερύψωσης (Maximum Overshoot) M_p
• Ideal integral compensation.
• Lag compensator.

• Ideal derivative compensation.
• Ideal derivative controller.

Στην ενότητα αυτή παρουσιάζεται μια γραφική τεχνική για τον υπολογισμό της ευστάθειας ενός συστήματος (κριτήριο ευστάθειας Nyquist).

Στην ενότητα αυτή αρχικά δίνουμε μια συνθήκη για να είναι πρώτα δύο πολυώνυμα μέσω της ορίζουσας Sylvester η οποία δημιουργείται από τους συντελεστές των πολυωνύμων που θέλουμε να ελέγξουμε. Στη συνέχεια προτείνουμε έναν αλγεβρικό τρόπο επίλυσης πάνω στον δακτύλιο των πολυωνύμων της διοφαντικής εξίσωσης a(s)x(s)+b(s)y(s)=c(s) με γνωστά τα πολυώνυμα a(s), b(s), c(s).

Κάνοντας χρήση της μεθόδου επίλυσης διοφαντικών εξισώσεων που παρουσιάσαμε στην ενότητα 15, προτείνουμε έναν τρόπο κατασκευής αντισταθμιστή για ένα κλειστό σύστημα αυτομάτου ελέγχου. Στην περίπτωση που έχουμε σύστημα με δύο εισόδους και δύο εξόδους προτείνουμε έναν τρόπο αποσύζευξης των εισόδων-εξόδων και αντιμετώπιση του προβλήματος σταθεροποίησης του συστήματος με τις τεχνικές που αναφέρθηκαν προηγούμενα.